Based on complex network theory, a new model has been imposed to study the common bidirectional selection phenomena in human society by Prof. WANG Binghong’s research group at University of Science and Technology of China (USTC), which was published on Dec. 19th in the Scientific Reports, the journal of the Nature Publish Group.

Bidirectional selection is a common phenomenon in nature and society, which appears in the process like choosing a mate between men and women, making contracts between job hunters and recruiters, and trading between buyers and sellers. It is very important to predict the matching results in these bidirectional selection systems, which can be discussed in the framework of complex networks. Particularly, many young single people are involved in online social networks, and they seek the other partner in social networks.

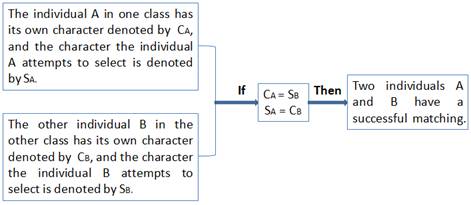
Figure 1: Model Mechanism (Image by WANG’s group)

The successfully matching rate of bidirectional selection system depends on the topological structure of social networks, Prof. WANG Binghong said, the leader of the research group of complex system. Analytical solution for the expectation of successfully matching rate on any given network was presented, which provides the theoretical understanding of underlying mechanisms of matching in complex networks. The matching performance has been quantitatively investigated on the Regular networks, Small-world networks, Random networks and Scale-free networks. The results revealed that the matching performance of the small-world networks is the best， indicating that the evolution of social network tends to be conducive to the matching among populations with the different gender. These results are helpful for researching the specific bidirectional selection system and explaining why matchmaking online for young people became so popular.

Figure 2: Successful matching between a boy and a girl (Image by WANG’s group)

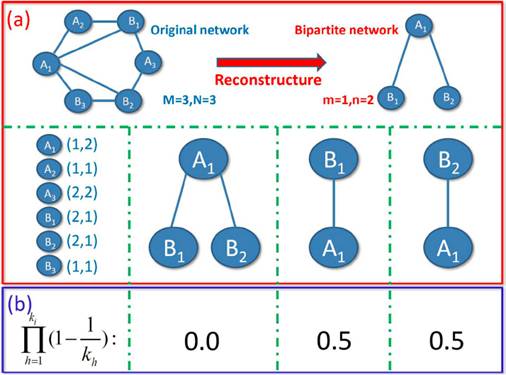
Figure 3: Illustration of the matching process. Upper panel (a) gives a simple example how the bipartite network is reconstructed, where node A1 in set A has two neighbors belonging to set B where B1 and B2 are matched with A1, m=1 and n=2. Compared to the original networks, only links of matched nodes are reserved in the reconstructed network. Here, A1 with character of (1, 2), B1 with character of (2, 1), and B2 with character of (2, 1) are reserved. The formulas denotes the probability that the node cannot match with its neighbors, and the value is 0.0 for A1, 0.5 for B1 1, and 0.5 for B2, as shown in panel (b). Then the expectations to match successfully for two sets A and B are calculated. (Image by WANG’s group)

The work is supported by the National Natural Science Foundation of China.
Paper Link:
Scientific Reports 4, 7577 (2014); Doi:10.1038/srep07577.
http://www.nature.com/srep/2014/141219/srep07577/full/srep07577.html#close 

Prof. WANG Binhong

Tel:  +86-551-3607407

Email: bhwang@ustc.edu.cn

(School of Physical Sciences)