When being cooled quickly, a liquid can turn into a glass instead of a crystal. The nature of glasses is one of the most challenging problems in condensed matter physics. Similarly, colloidal suspensions can form colloidal glasses upon the fast increase of the packing density. Compared to atomic and molecular systems, colloidal systems have much larger particle size and much slower particle motion, so they have become ideal model systems to study the glass transition. Among all colloidal systems, hard-sphere systems are widely used due to the simple inter-particle potential.

In a hard-sphere glass, particles vibrate around their equilibrium positions for a long time, not being able to escape easily. When being quenched to zero temperature, however, the system loses its rigidity at once because particles are not in contact, until the packing density reaches the random close packing density where the jamming transition happens. Recent studies have shown that the glass transition density of hard spheres is lower than the jamming transition density. Then properties of hard-sphere glasses lying between these two transitions are perplexing: They are disordered solids under thermal excitations, but not in the absence of dynamics. What is the origin of this strange behavior of hard-sphere systems? What are the challenges of hard-sphere glasses to our common views of solids?

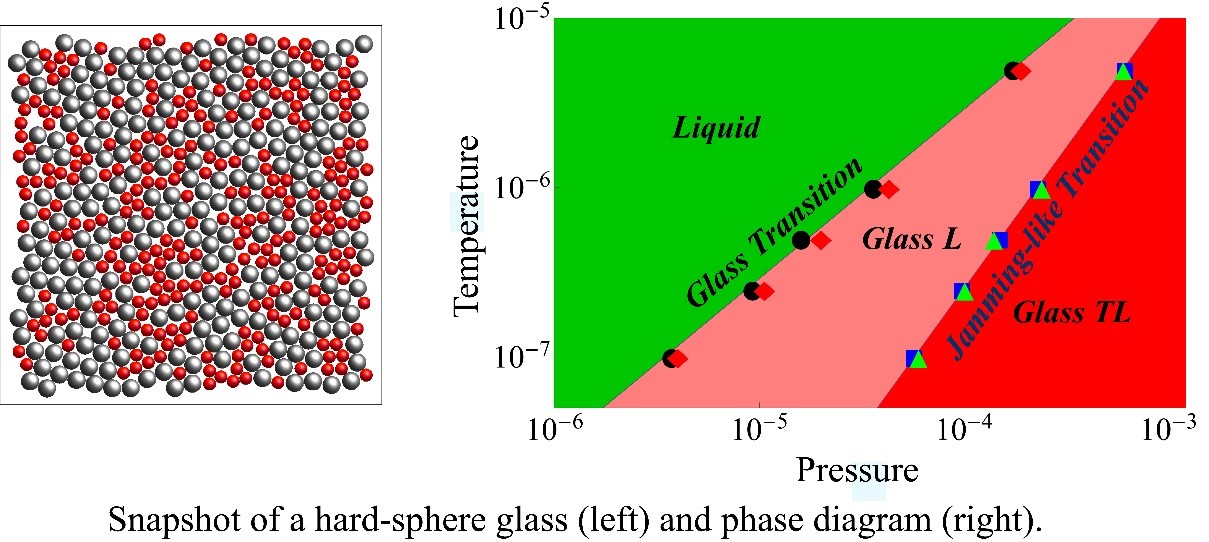
The group led by Prof. Ning Xu at the CAS Key Laboratory of Soft Matter Chemistry, Hefei National Laboratory of Physical Sciences at the Microscale, and Department of Physics, University of Science and Technology of China revealed the nature of hard-sphere glasses in their recent paper published in Physical Review Letters on January 23 [Phys. Rev. Lett. 114, 035502 (2015)]: Hard-sphere glasses are disordered solids without well-defined transverse phonons.

Due to the structural disorder, phonons are strongly scattered in glasses. When the phonon wavelength is comparable to its mean free path, the Ioffe-Regel limit is reached. Beyond the Ioffe-Regel frequency, normal modes of vibration cannot be strictly defined as phonons because the wavelength will be larger than the mean free path. By calculating the dynamical structural factors of glasses composed of soft particles with repulsions, PhD candidate Xipeng Wang et al. of the group obtained the Ioffe-Regel limits. Their previous studies have shown that the same model systems undergo the glass transition and jamming-like transition in sequence upon compression at fixed temperature. In the zero-temperature limit, these two transitions correspond to the glass transition and jamming transition of hard spheres. In this work, they found that glasses above the jamming-like transition (denoted as glass TL) can carry well-defined transverse and longitudinal phonons with both the transverse and longitudinal Ioffe-Regel frequencies greater than zero. Interestingly, the transverse and longitudinal Ioffe-Regel frequencies drop to zero at the jamming-like transition and glass transition, respectively. Glasses between the two transitions (denoted as glass L), which are hard-sphere glasses in the zero-temperature limit, can only carry well-defined longitudinal phonons.

Because normal modes of vibration are fundamental to properties of solids, the absence of well-defined transverse phonons should be the intrinsic cause of the extraordinary behaviors of hard-sphere glasses mentioned above. By calculating the elastic moduli, they also found that the ratio of the shear modulus to the bulk modulus of hard-sphere glasses decreases with increasing packing density and decays to zero at the jamming transition, which is opposite to the packing density dependence of soft-sphere glasses above the jamming transition. This difference is the direct manifestation of the special nature of hard-sphere glasses. The absence of well-defined transverse phonons in hard-sphere glasses is a surprising finding, which challenges our knowledge about solids and implies that using hard-sphere systems to understand the glass transition of atomic and molecular systems may be problematic.

This work is supported by the National Natural Science Foundation of China, the Ministry of Science and Technology of China, and the Chinese Academy of Sciences.

Link to the paper: http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.114.035502

(XU Ning,School of Physical Sciences)