Recently, Prof. QIAO Zhenhua’s group in Hefei National Laboratory for Physical Sciences at the Microscale and Department of Physics of USTC and collaborators made a great progress in the field of counterintuitive current partition law at the topological intersection. The results are published in Physical Review Letters, an international top journal of physics [Phys. Rev. Lett. 112, 206601 (2014)].
Various topological effects, e.g., topological insulators, quantum anomalous Hall effect, quantum valley Hall effect, etc. have attracted much attention in the fields of conduced matter physics and materials physics. One of the important features of these topological phases is that the bulk is insulating, however, the edges/surfaces are conducting. Usually, the topological property of an experimentally fabricated material is not uniform [schematically shown in Fig. (a)]. “+/-” are used to represent different domains characterized by different topological indexes. At the interface of two domains with different topological indexes, topologically confined one-dimensional states are formed. These states possess intriguing transport properties – the backscattering is strongly suppressed, as Prof. Qiao and his collaborators found previously, due to the chiral-propagation and wide spread of wavefunction [Nano Lett. 11, 3453 (2011)]. This makes the topological confined state a good candidate for dissipationless electronic devices. Another interesting and important question appears in the real application: when the current comes to a bifurcation point, how will the current propagate and split?
To address this question, Prof. Qiao and his collaborators studied the current partition law at a four-terminal topological intersection in a bilayer graphene system. Through numerical simulation, they find a counterintuitive current partition law depending solely on the geometry of the system. For the simplest case as illustrated in Fig. (b), the incoming current from the right terminal split equally along the up and down terminals due to the symmetry, whereas the forwarding current into the left terminal is zero due to the chiral propagating property. As the right terminal rotates counterclockwise a certain angle as shown in Fig. (c), however, the current partition prefers the path with a larger rotation angle. Cases are similar when the right terminal rotates clockwise. Moreover, even though there is no current flows into the left terminal, its spatial position strongly influences the current partition. They also state that these phenomena originate from the overlap and interference effect between the wavefunctions in these four terminals. These intriguing properties will benefit the construction and application of topological-network based dissipationless current splitter and quantum interference devices.
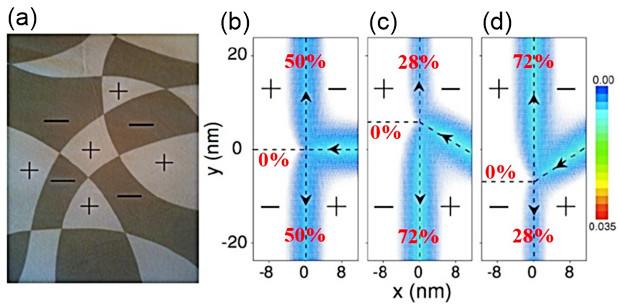
(a) Schematic of topological network. The domains with different topological indexes are labelled by +/-. (b)-(d). Current partitions when the angles between the right terminal and the down one are 90°, 60°, and 120°, respectively. The number in each terminal means the relative current strength for outgoing terminals.
This work was financially supported by USTC Startup, Bairen Program of Chinese Academy of Sciences and National Natural Science Foundation of China.
(QIAO Zhenhua,School of Physical Sciences)